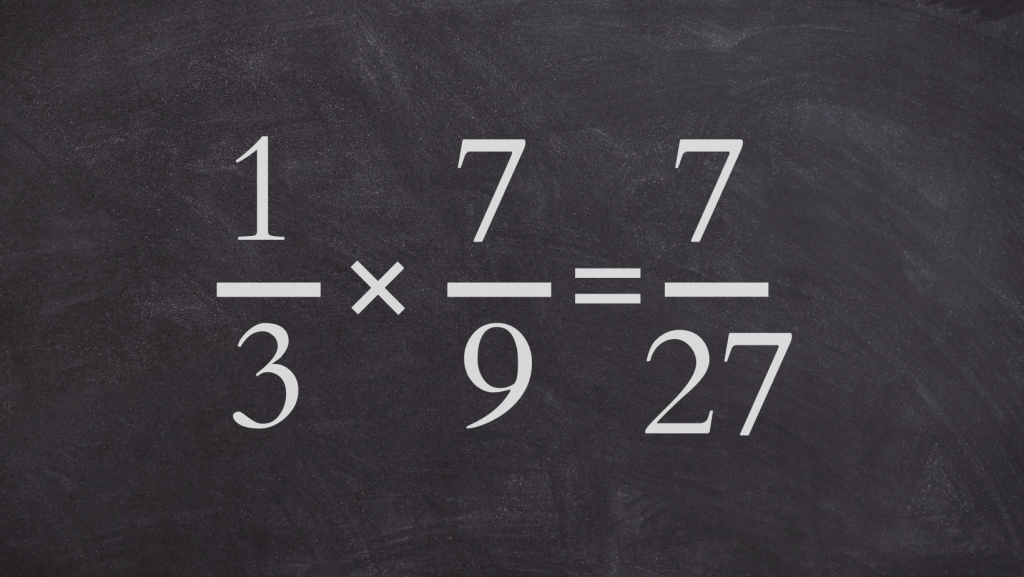Ułamki to podstawowe pojęcie matematyczne, które praktycznie każdy uczeń spotyka już na początku edukacji szkolnej. Są to liczby, które mają postać ilorazu dwóch innych liczb. Choć ułamki mogą wydawać się prostymi obliczeniami, często sprawiają wiele trudności w zrozumieniu i obliczeniach. Jednym z powodów jest duża ilość typów ułamków i reguł, jakie trzeba znać, aby poprawnie je obliczać. W analityce matematycznej wyróżnia się różne rodzaje ułamków, takich jak właściwe, niewłaściwe, dziesiętne, okresowe i wiele innych. Naucz się ich i raz na zawsze pożegnaj się z problemami matematycznymi.
Jakie są rodzaje ułamków?
Istnieją trzy podstawowe rodzaje ułamków:
- Ułamki zwykłe – składają się z dwóch liczb całkowitych zapisanych jedna nad drugą ukośną kreską, np. 3/4.
- Ułamki dziesiętne – zapisywane jako ułamek zwykły, w którym mianownik jest potęgą dziesiątki, np. 0,25 to ułamek dziesiętny 1/4.
- Ułamki mieszane – składają się z liczby całkowitej oraz ułamka zwykłego, np. 2 1/4.
Dodatkowo istnieją również ułamki dziesiętne okresowe, w których występuje okresowo powtarzający się ciąg cyfr po przecinku.
Co to jest odwrotność ułamka?
Odwrotność ułamka to liczba, która po wymnożeniu przez dany ułamek daje 1. Innymi słowy, odwrotna liczba do ułamka a/b to b/a. Dla przykładu, odwrotnością ułamka 2/5 jest 5/2, a odwrotnością ułamka 3/4 jest 4/3. Odwrotność ułamka jest bardzo ważna w matematyce, ponieważ często wykorzystywana jest w obliczeniach i równaniach. Jest również kluczowym elementem w dzieleniu ułamków. Aby podzielić jeden ułamek przez drugi, odwraca się drugi ułamek i mnoży go przez pierwszy. Na przykład, aby podzielić 2/5 przez 3/4, odwraca się drugi ułamek, otrzymując 4/3 i mnoży się go przez pierwszy ułamek, co daje wynik 8/15. Jest to niezwykle proste i przydatne, dlatego warto poświęcić kilka chwil, aby przyswoić tą wiedzę i poćwiczyć liczenie tego typu działań.
Jak się dodaje ułamki zwykłe, odejmuje i mnoży przez siebie?
Aby dodać lub odjąć dwa ułamki zwykłe, musimy upewnić się, że mianowniki są takie same. Jeśli nie są, musimy sprowadzić ułamki do wspólnego mianownika.
- Sprowadzanie ułamków do wspólnego mianownika:
- Znajdź najmniejszą wspólną wielokrotność mianowników
- Każdy ułamek przedstaw w taki sposób, aby jego mianownik był równy najmniejszej wspólnej wielokrotności
- Dodawanie i odejmowanie ułamków o wspólnym mianowniku:
- Dodaj lub odejmij liczniki ułamków, a mianownik pozostaw bez zmian
- Upewnij się, że wynik jest uproszczony do postaci nieskracalnej
Przykład dodawania ułamków:

Mnożenie ułamków zwykłych:
Aby pomnożyć dwa ułamki zwykłe, wymnóż liczniki i mianowniki, a następnie uproszcz wynik do postaci nieskracalnej.
Przykład mnożenia ułamków: