Twierdzenie Pitagorasa to jedno z najważniejszych twierdzeń matematycznych, znane i wykorzystywane od tysięcy lat. Jest to fundamentalna zasada geometrii płaskiej, która opisuje związek między długościami boków prostokątnego trójkąta. Jest to nie tylko ważne narzędzie w matematyce, ale także znajduje zastosowanie w innych dziedzinach nauki, takich jak fizyka, astronomia czy architektura. Dowiedz się jakie są wzory twierdzenia Pitagorasa i jak ich używać.
Co to jest twierdzenie Pitagorasa?
Twierdzenie Pitagorasa to jedno z najważniejszych twierdzeń matematycznych, które opisuje związek między bokami trójkąta prostokątnego. W skrócie mówiąc, mówi ono, że kwadrat długości przeciwprostokątnej trójkąta prostokątnego jest równy sumie kwadratów długości przyprostokątnych. Twierdzenie to zostało nazwane imieniem greckiego matematyka Pitagorasa, który żył w VI wieku p.n.e. i jest uważany za jego odkrywcę. Twierdzenie Pitagorasa odgrywa ważną rolę w matematyce, ponieważ jest nie tylko kluczowym elementem geometrii płaskiej, ale także znalazło zastosowanie w innych dziedzinach, takich jak fizyka czy architektura. Dlatego też, zrozumienie i umiejętność stosowania tego twierdzenia jest kluczowe dla wielu dziedzin nauki i praktycznych zastosowań.
Wzory twierdzenia Pitagorasa
Twierdzenie Pitagorasa to jedno z najważniejszych twierdzeń matematycznych, które od wieków zachwyca swoją prostotą i uniwersalnością. Mówi ono, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Jest to twierdzenie, które znajduje zastosowanie nie tylko w matematyce, ale także w innych dziedzinach nauki, jak na przykład w fizyce czy architekturze. Istnieje wiele sposobów, aby przedstawić wzory twierdzenia Pitagorasa. Najbardziej klasyczna postać brzmi:
- a^2 + b^2 = c^2, gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.
Jednak istnieją również inne wersje wzorów, takie jak:
- Długość przeciwprostokątnej trójkąta prostokątnego jest równa pierwiastkowi kwadratowemu z sumy kwadratów długości przyprostokątnych:
c = sqrt(a^2 + b^2)
- Długość jednej z przyprostokątnych trójkąta prostokątnego jest równa pierwiastkowi kwadratowemu z różnicy kwadratu długości przeciwprostokątnej i kwadratu długości drugiej przyprostokątnej:
a = sqrt(c^2 – b^2)
- Długość drugiej przyprostokątnej trójkąta prostokątnego jest równa pierwiastkowi kwadratowemu z różnicy kwadratu długości przeciwprostokątnej i kwadratu długości pierwszej przyprostokątnej:
b = sqrt(c^2 – a^2)
Wszystkie te wzory są równie poprawne i pozwalają na łatwe obliczanie długości boków trójkąta prostokątnego.
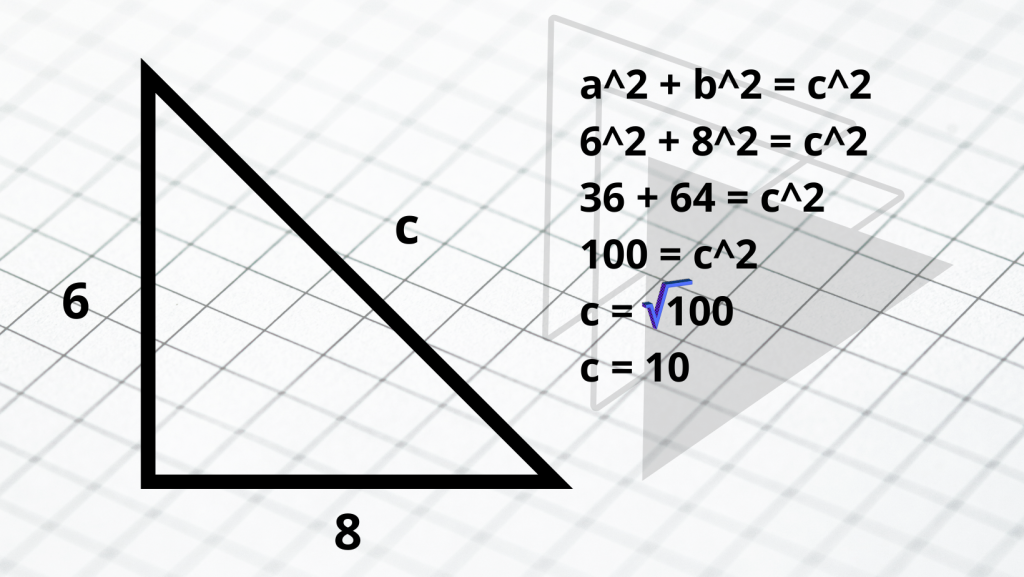
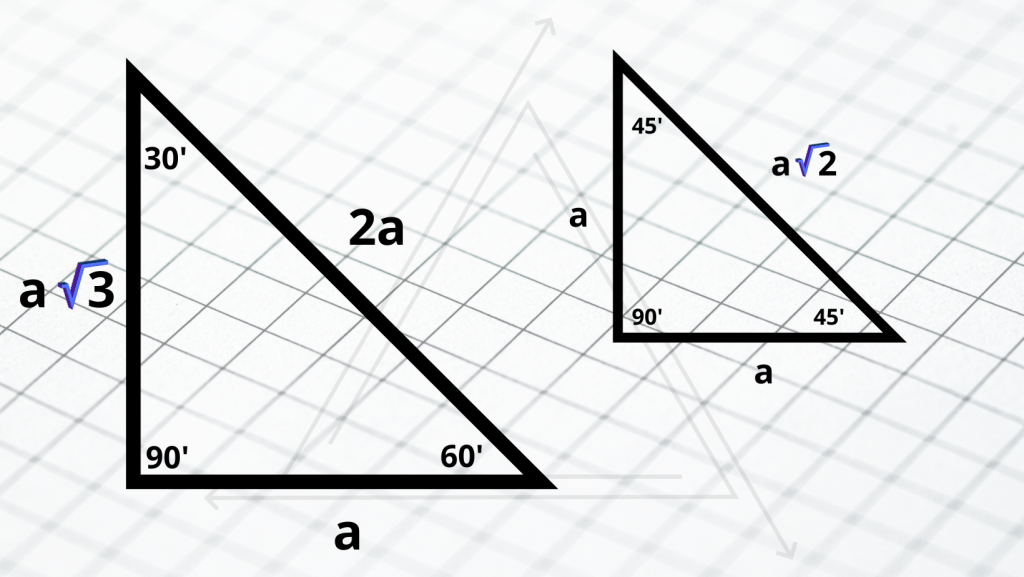
Jak obliczyć kąt w trójkącie prostokątnym?
Aby obliczyć kąty w trójkątach prostokątnych o kątach 30’, 60’, 90’ oraz 90’, 45’, 45’ wystarczy używać danych z poniższej grafiki. W momencie gdy bok a ma przykładowo 5 cm wystarczy podstawić tą wartość w miejsce a we wzorze. Jest to niezwykle proste, dlatego naprawdę warto nauczyć się tych własności, ponieważ mogą one być pomocne na egzaminach, sprawdzianach i w życiu codziennym.